Day02

空间滤波基础

• 滤波的原理： 空间滤波是采用滤波处理的图像增强的方法，理论基础是空间卷积和空间相关，目的是改善图片质量

• 线性空间滤波

  • 移动滤波的模板w称为滤波器
  • 相关 与 卷积：
    相关是指模板w按下图所示的方式进行图像数组的处理。在原理上，卷积是相同的处理过程，只不过在w通过之前先将它选旋转180度
    
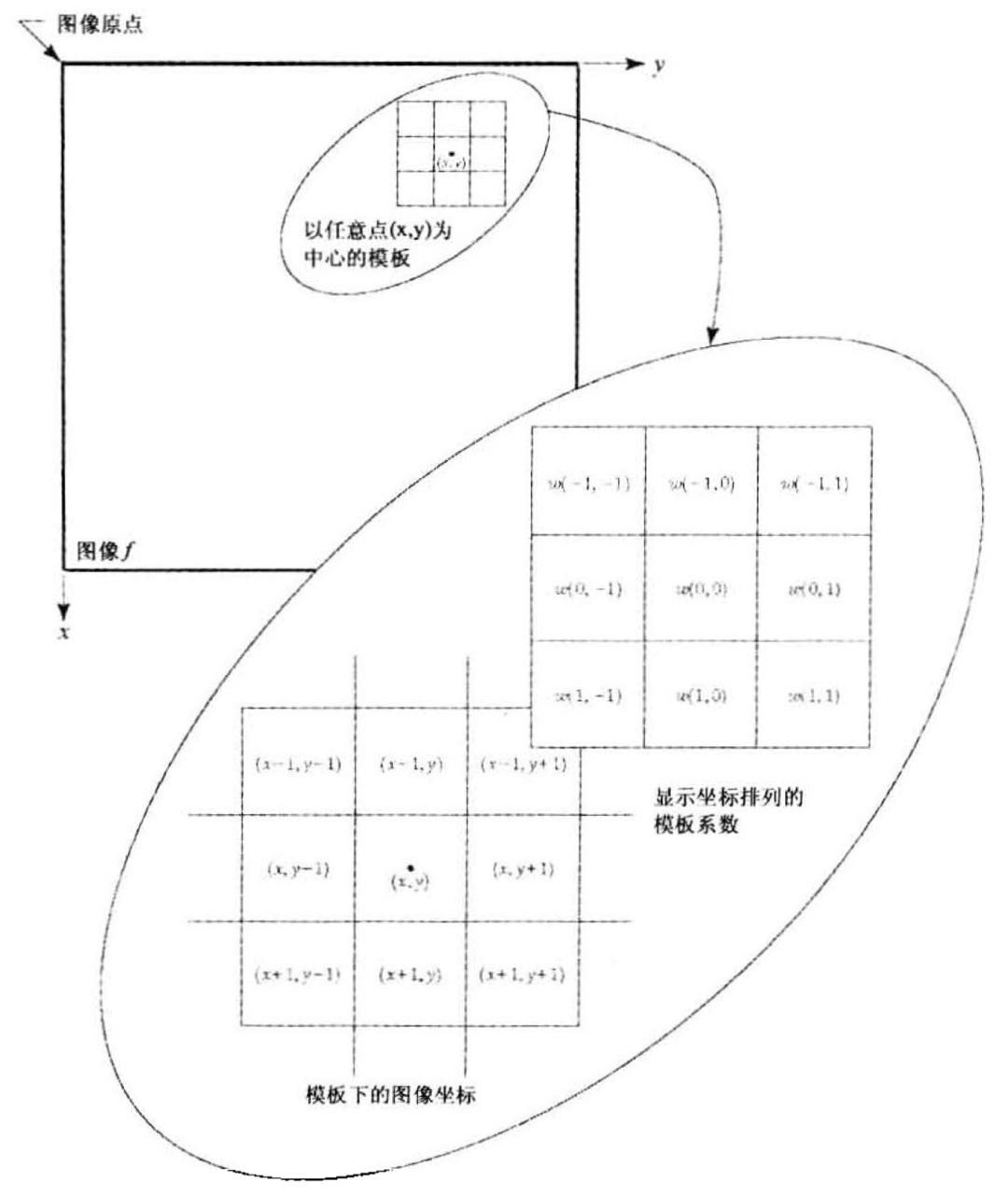
    相关与卷积操作说明
    
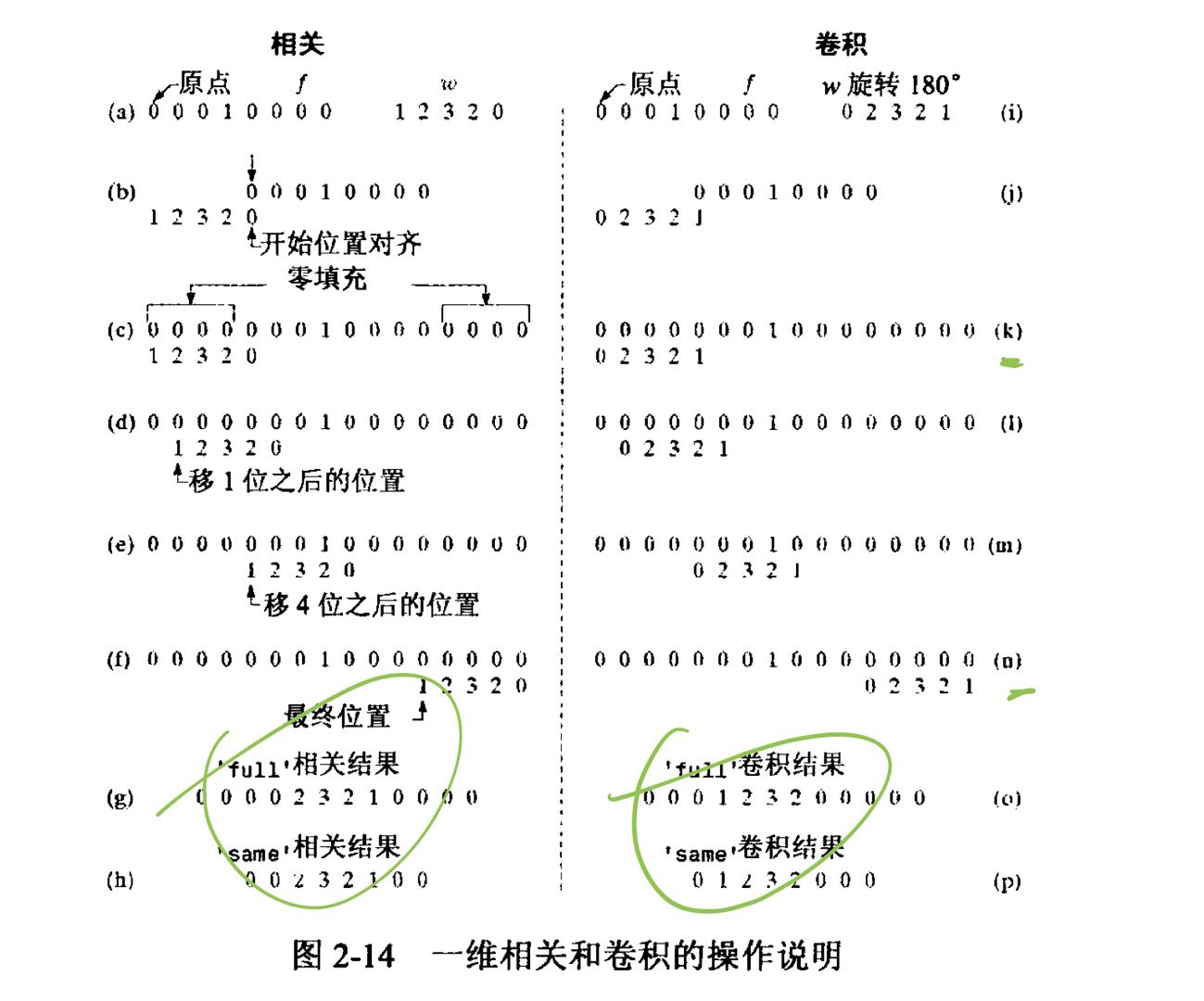
    需要注意的地方：
    1. 相关是滤波器位移的函数
    2. 滤波器w与一个只包含一个1其余全是0的函数相关，得到的是旋转了180度的滤波器w，将这个函数称之为离散单位冲激
       结论: 一个函数与离散单位冲激相关，在该冲激位置产生这个函数的一个翻转版本
       一个函数与离散单位冲激相关激卷积，得到的是在该冲激处的这个函数的拷贝，这个复制的性质称为筛选
       这种定义推广到图像如下图所示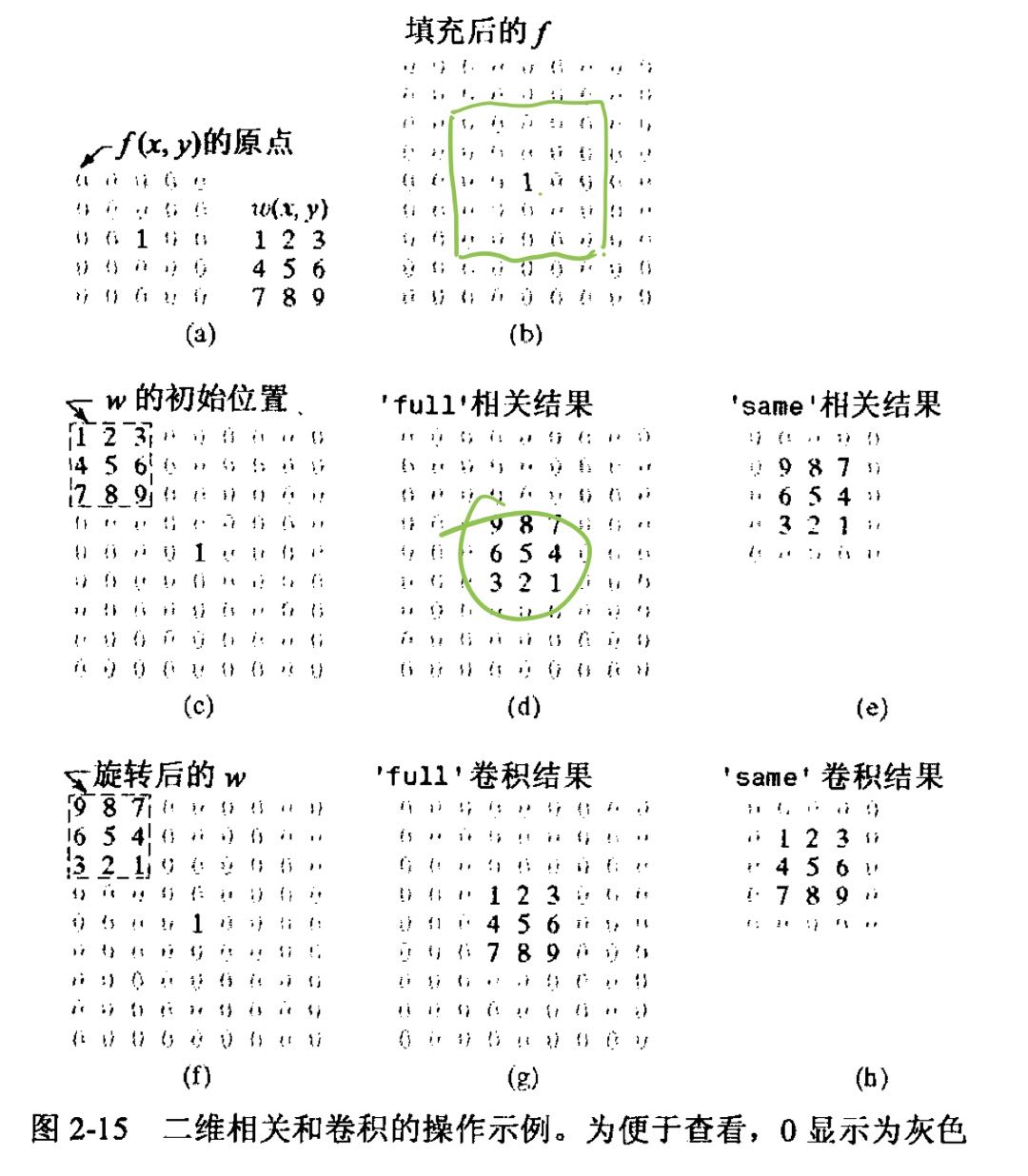
       
       为了便于表达，以公式形式总结两种形式
    • 大小为m×n的滤波模板w(x,y)与函数f(x,y)的相关
      
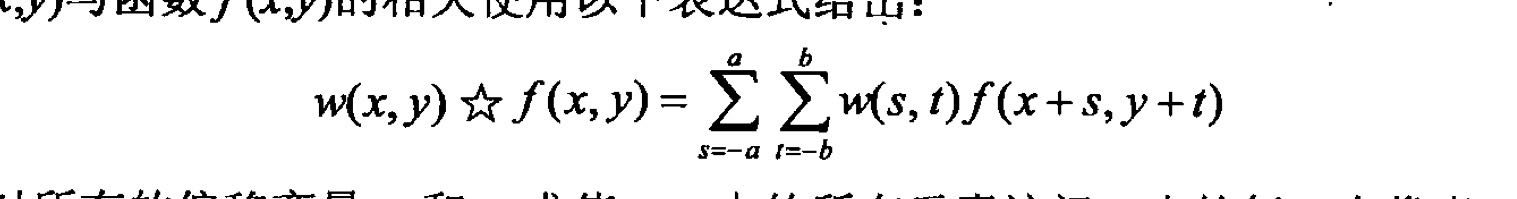
    • 大小为m×n的滤波模板w(x,y)与函数f(x,y)的卷积 $$w(x,y)\bigstar f(x,y)=\sum_{s=-a}^{a}\sum_{t=-b}^{b}w(s,t)f(x+s,y+t)$$

  • Matlab的实现:
    工具箱使用imfilter来实现线性空间滤波，语法如下:

    g = imfilter(f, w, filtering_mode, boundary_options, size_options)

    默认值为相关，若想执行卷积操作，有以下两种做法：

    g = imfilter(f, w, 'conv')

    或者使用rot90(w, 2)来将w旋转180度

    g = imfilter(f, rot90(w, 2))

    f是输入图像，w为滤波模板，g为滤波结果
    其他参数如下
    
    使用matlab实现为

    f = imread('filter.jpg');
    F = im2double(f);
    imshow(F);
    title('current image');
    
    w = ones(31);
    gd = imfilter(F, w);
    figure,imshow(gd, [ ]);
    title('Default');
    
    gr = imfilter(F, w, 'replicate');
    figure,imshow(gr, [ ]);
    title('replicate');
    
    gs = imfilter(F, w, 'symmetric');
    figure,imshow(gs, [ ]);
    title('symmetric');
    
    gc = imfilter(F, w, 'circular');
    figure,imshow(gc, [ ]);
    title('circular');
    
    g = imfilter(f, w, 'replicate');
    figure,imshow(g, [ ]);
    title('replicate unit8');

    这里开始读取的filter.jpg为uint8格式，故在处理之前先使用im2double将其转化为double类型以提高精度
    滤波结果如下
    

• 非线性空间滤波：
  线性空间滤波基于计算乘积和，即线性操作，非线性空间滤波基于涉及邻域像素内的非线性操作，例如，使每个中心点的响应等于邻域内像素最大值的操作可以称为是非线性滤波操作
  • Matlab工具
    1. nlfilter：直接执行二维操作
    2. coldilt：按列组织数据，更多采用