Day03

标准的空间滤波器

线性空间滤波器

• 可以使用fspecial实现，生成滤波器w

  w = fspecial('type', parameters)

  ‘type’表示滤波器的类型，’parameters’进一步定义指定的滤波器
  应用参数如下：
  
  

• Laplace滤波器的实现

  • 原理：
    图像f(x,y)的laplace算子：
    
    Laplace算子增强公式：

    $$g(x,y) = f(x,y)+c[\triangledown ^2 f(x,y)]$$

    注意：如果模板的中心系数为正，c为1;如果为负，c为0.

    fspecial('laplacian', alpha)

    可以实现更为一般的laplace模板

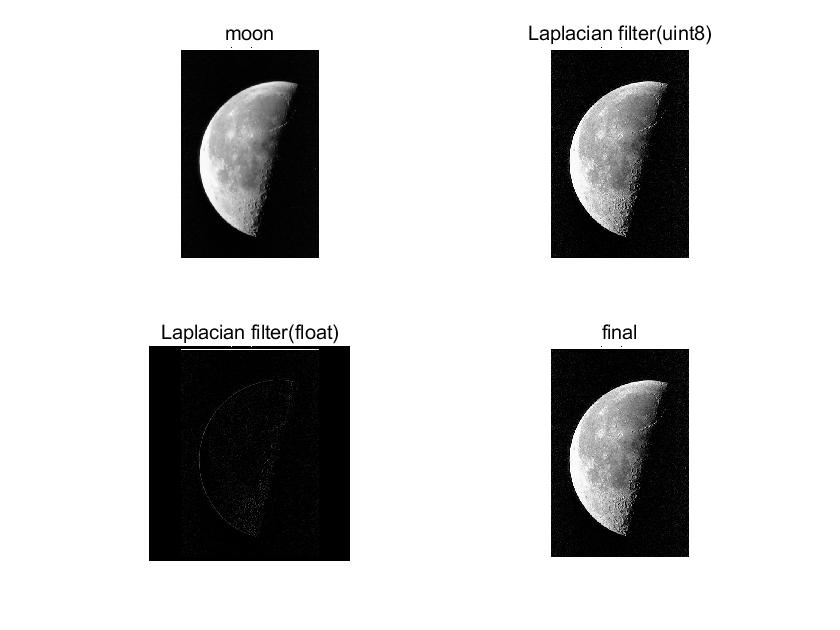
  • 下面是用laplace滤波器增强图像的例子：
    首先设置滤波器

    >> w = fspecial('laplacian', 0);

    

    输入的图像为unit8类，

    >> g1 = imfilter(f, w, 'replicate');
    >> imshow(g1);

    得到结果，但存在问题，所有像素都是正的。原因：滤波器的中心参数为负值，为了解决这一问题，可以在滤波前将f转换为浮点数

    >> ff = tofloat(f);
    >> g2 = imfilter(ff, w, 'replicate');
    >> imshow(g2);

    这里tofloat为M-IPT函数，实现代码如下：

    function [out,revertclass] = tofloat(inputimage)
    %Copy the book of Gonzales
    identify = @(x) x;
    tosingle = @im2single;
    table = {'uint8',tosingle,@im2uint8
    'uint16',tosingle,@im2uint16
    'logical',tosingle,@logical
    'double',identify,identify
    'single',identify,identify};
    classIndex = find(strcmp(class(inputimage),table(:,1)));
    if isempty(classIndex)
    error('不支持的图像类型');
    end
    out = table{classIndex,2}(inputimage);
    revertclass = table{classIndex,3};

    导入workspace即可

    最后用原始图像减去laplace图像来恢复失去的灰度层次(因为中心参数为负值)

    >> g = ff - g2;
    imshow(g);

    可以看到结果比原图象要清晰
    

    非线性空间滤波器

• 函数ordfilt2计算统计排序(order-statistic filter)滤波器(也叫做rank filter,即排序滤波器)
  语法为：

  g = ordfilt2(f, order, domain)

用邻域集合中的第order个元素去替换f中的每个元素的值来生成图像g，domain是由0和1组成的大小为m×n的矩阵，规定了在计算中使用的邻域中像素点的位置

• 中值滤波器，最著名的统计排序滤波器，对应第50个百分位，对应奇数的m和n

  g = ordfilt2(f, (m*n + 1)/2, ones(m, n));

  • 这里提供了一个专门的二维中值滤波器:

    g = medfilt2(f, [m, n], padopt)

    padopt规定了三个可能的边缘填充选项:

  1. ‘zeros’,默认值
  2. ‘symmetric’,f按照镜像反射方式对称地沿边缘扩展
  3. ‘indexed’，f属于double类，用1填充;否则用0填充

  • 中值滤波增强图像:
    首先给图像添加黑白噪点发生概率为0.2的’椒盐噪声’

    >> fn = imnoise(f, 'salt & pepper', 0.2)

    对带噪图像进行中值滤波处理

    >> gm = medfilt2(fn)

    注意，在这里出现了错误，==A应为二维==
    

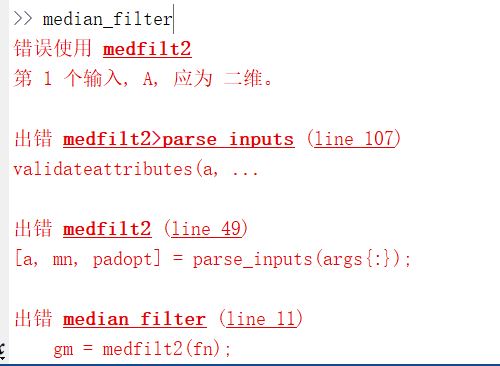
    原因:中值滤波medfilt2,输入的图像应为二维矩阵，实际输入的为imread读取的图像加上噪声，通常是三维RGB图，是三维矩阵
    解决办法:先用rgb2gray(f)将图像转换为灰度矩阵图像

    >> fn2 = rgb2gray(fn);
    >> gm = medfilt2(fn2);
    >> imshow(gm);

    减弱外圈黑点

    >> gms = medfilt2(fn2, 'symmetric');