Day04

频域滤波

1. 对图像平滑的低通滤波
2. 对图像锐化的高通滤波
3. 去除周期的选择性滤波

二维傅里叶变换

• 二维傅里叶变换:

  $$F(u,v)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x,y)e^{-j2\pi(ux + vy)}\,\mathrm{d}x \mathrm{d}y$$

• 二维傅里叶逆变换：

  $$f(x,y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} F(u,v)e^{j2\pi(ux + vy)}\,dxdy$$

二维离散傅里叶变换

f(x,y)代表一幅大小为M×N的图像，其中x=0,1,……,M-1,y=0,1,…..,N-1,DFT如下

$$F(u,v)=\int_{x=0}^{M-1} \int_{y=0}^{N-1} f(x,y)e^{-j2\pi(\frac{ux}{M}+\frac{vy}{N})}\,\mathrm{d}x \mathrm{d}y$$

IDFT：

$$f(x,y)=\frac{1}{MN}\int_{x=0}^{M-1} \int_{y=0}^{N-1} F(u,v)e^{j2\pi(\frac{ux}{M}+\frac{vy}{N})}\,\mathrm{d}x \mathrm{d}y$$

这里的F(u,v)被称为展开的傅里叶级数

频域原点出的变换的值F(0,0)称为傅里叶变换的直流(dc)分量，F(0,0)等于f(0,0)平均值的MN倍。要注意的是在MATLAB中索引是从1开始的而不是从0开始的

MATLAB实现对图像的Fourier变换和逆变换

• Fourier变换，f为原图像

  >> F = fft2(f);

• Fourier谱

  >> S = abs(F);

该函数计算的是数组中每个元素的幅值( $ \sqrt{r^2+i^2} $ )
可以在这里观察到4个角的亮点，这就是周期特性的结果，不便观察

• 将交换的原点移动到频域矩形的中心

  >> Fc = fftshift(F)

频谱范围大，不边观察

• 取模，缩放

  S2 = log(1 + abs(Fc));

• Fourier逆变换

  >> f = ifft2(F);

下面是完整代码

img=imread('moon.jpg');
subplot(2,2,1);
    imshow(img);
    title('原图');
    
f=rgb2gray(img);    %对于RGB图像必须做的一步，也可以用im2double函数
F=fft2(f);          %Fourier变换
F1=log(abs(F)+1);   %取模,缩放
subplot(2,2,2);
    imshow(F1,[]);
    title('傅里叶变换频谱图');
    
Fs=fftshift(F);      %将频谱图中零频率成分移动至频谱图中心
S=log(abs(Fs)+1);    %取模并进行缩放
subplot(2,2,3);
    imshow(S,[]);
    title('频移后的频谱图');
    
fr=real(ifft2(ifftshift(Fs)));  %频率域反变换到空间域，并取实部
ret=im2uint8(mat2gray(fr));    %更改图像类型
subplot(2,2,4);
    imshow(ret);
    title('逆傅里叶变换');

结果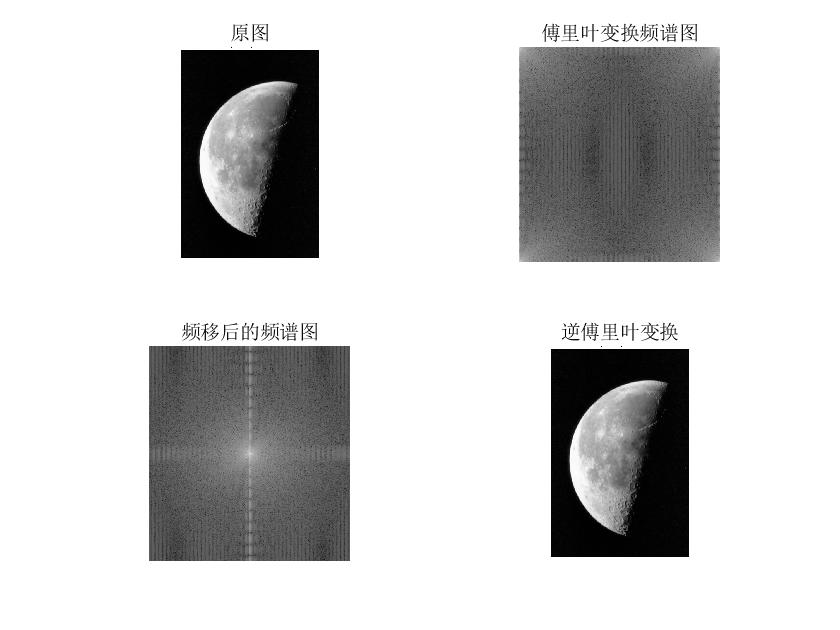

如果使用>> f = im2double(img)进行处理，则会出现以下结果

-分析

1. 图像Fourier变换之后立即imshow会报错
   
   这是因为经过fourier变换之后的图像矩阵为复数矩阵，包含实部和虚部，此时进行abs(f)取复数矩阵的模，再显示。
2. rgb2gray()和im2double()的使用
   这一点要特别注意，对于RGB图像，imread()是已三维矩阵的形式来存储的，要先进行类型转换，否则会出现空白
3. rgb2gray()转换为灰度图像,得到的图像呈灰色基调，见‘结果’
4. im2double()转换成双精度图像，得到的图像呈白色基调，见‘结果’
   其他图像处理结果
   

可以看到Fourier逆变换处理之后的图片为原图的灰度图片。

对图像Fourier变换的意义分析

对于一个图像，其频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间的梯度。设f为一个能量有限的模拟信号，其傅里叶变换代表f的频谱。从纯粹的数学意义上来看，Fourier变换是将一个函数转换成一系列的周期函数来进行处理的。从物理角度来看，Fourier变换是将图像从空间域转换到频率域，逆变换是将图像从频率域转换到空间域。也就是说，Fourier变换是将图像的灰度分布函数变换成图像的频率分布函数。==这里要注意是灰度分布函数==,下面还会说到。

Fourie逆变换是将图像的频率分布函数转换成灰度分布函数(原始图像的灰度分布函数),图像的概念前边说过，用一个二维矩阵来表示空间上的各点，z=f(x,y)，但空间是三维的，因此空间上的物体在另一个维度上的关系必须由梯度来表示。

Fourier频谱图上的明暗点，意义是指图像上的某一点与邻域点差异的强弱，即梯度的大小。

对频谱移频到原点之后，可以看出图像的频率分布是以原点为圆心，对称分布的.