形态学图像处理
从这里开始过渡,从输入输出都是图像,过渡到图像分析方法,输出以某种方法来描述图像的内容。
集合理论基础
令Z为整数集合,用于产生的数字图像的抽样处理可以看做是把xy平面分割成网格状,其中每个网格的中心坐标是来自笛卡尔积$Z^2$中的一对元素。在集合理论中,如果(x,y)是来自$Z^2$的整数,f是分配给每个不同坐标的对(x,y)的亮度值的映射,那么函数f(x,y)被成为数字图像。如果亮度值也为整数,那么这幅图像就变成了二维图像。
集合的基本操作:$\in$,$\notin$,$\cup$,$\cap$,+,-.除了这些基本操作,形态学操作还需要两个算子,他们特别针对元素均为像素坐标的集合
- 集合的反射$\hat{B}$
- 点z=($z_1$,$z_2$)集合的平移${(A)}_z$
二值图像、集合及逻辑算子
形态学理论把二值图像看成是前景(1值)像素的集合,集合的元素属于$Z^2$如果A和B都是二值图像,那么$C=A\cup B$也是二值图像在MATLAB中使用逻辑表达式在二值图像上进行逻辑运算
| 集合运算 | 二值图像的MATLAb语句 | 名称 |
|---|---|---|
| $A\cap B$ | A & B | 与 |
| $A\cup B$ | A $\rvert$ B | 或 |
| $A^c$ | ~B | 非 |
| $A-B$ | A &~ B | 差 |
腐蚀和膨胀
膨胀
膨胀是使图像中的目标”生长”或”变粗”的操作。程度由一种被称为结构元的形状来控制
A被B膨胀,表示为$A \oplus B$,作为集合操作
约定: $A \oplus B$ 的第一个操作数是图像,第二个操作数是结构元,结构元通常比图像小的多。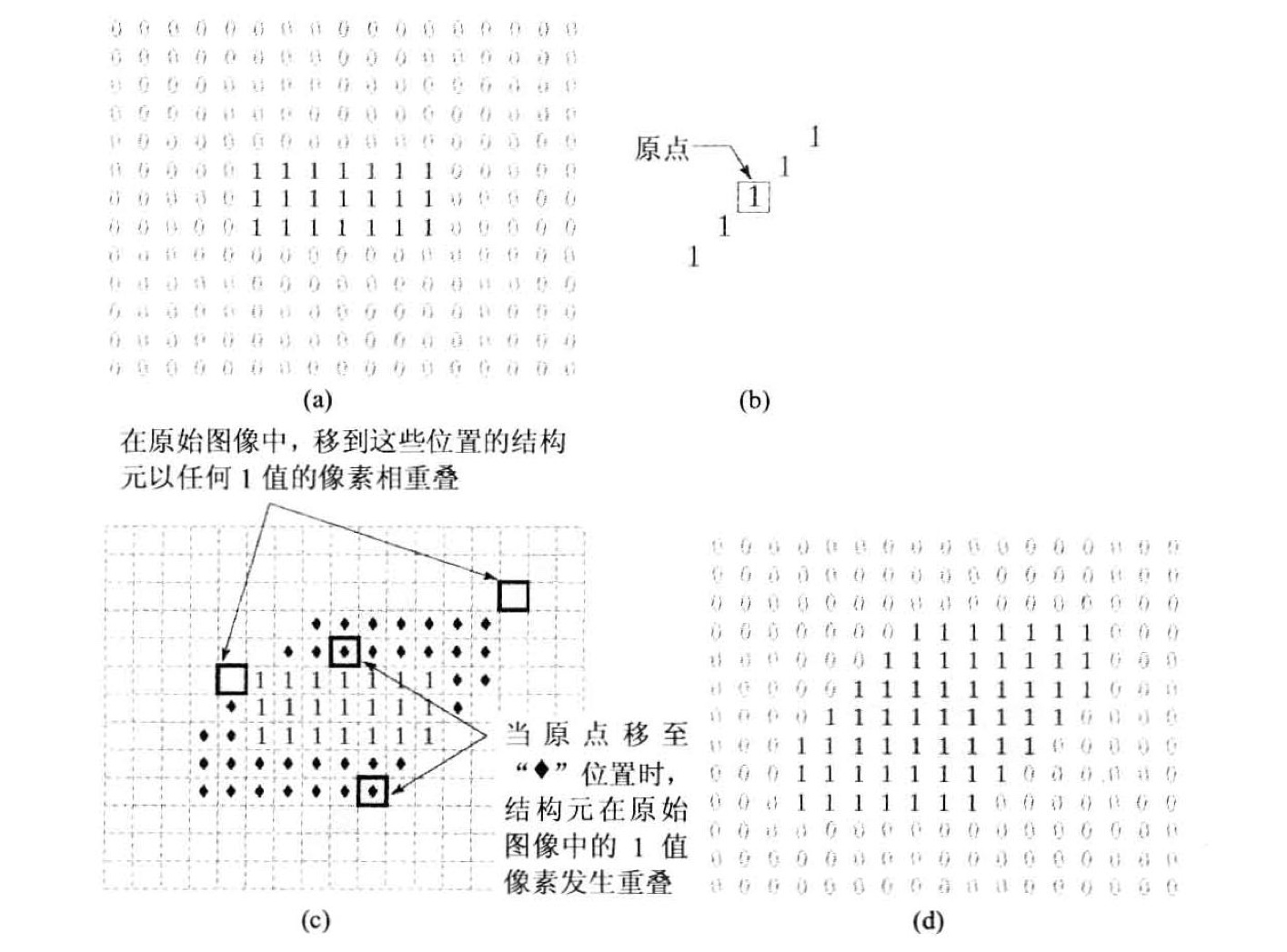
- 工具箱函数imdilate(A, B)来执行膨胀
1
2
3
4
5
6
7f = imread('1111.jpg');
B = [0 1 0; 1 1 1; 0 1 0];%自定义结构元
D = imdilate(f, B);
subplot(1,2,1),imshow(f);
title('原图')
subplot(1,2,2),imshow(D);
title('膨胀后的图')

腐蚀
腐蚀”收缩”或”细化”二值图像中的物体。像膨胀一样,收缩的方法和程度由结构元控制。
A被B腐蚀表示为$A\ominus B$,定义为:
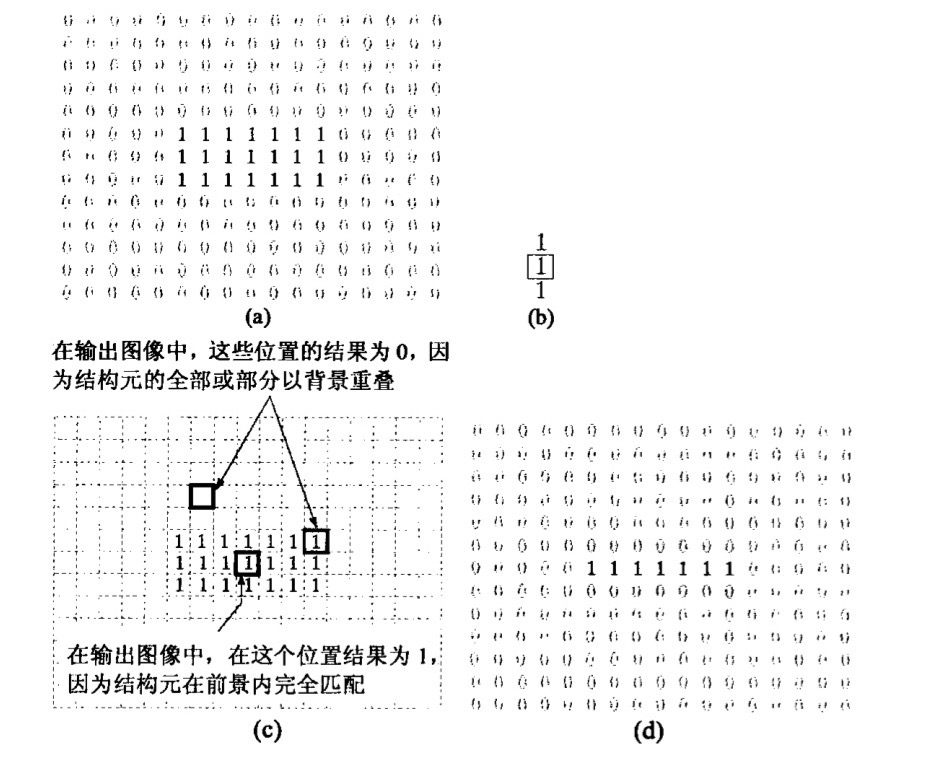
工具箱函数imerode(A,B)来执腐蚀1
2
3
4
5
6
7f = imread('tig.jpg');
B = [0 1 0; 1 1 1; 0 1 0];%自定义结构元
R = imerode(f, B);
subplot(1,2,1),imshow(f);
title('原图')
subplot(1,2,2),imshow(R);
title('腐蚀后的图')

结构元
strel函数,用来构造各种大小和形状的结构元1
se = strel(shape, parameters);
shape是希望形状的字符串,parameters是描述形状信息的参数列表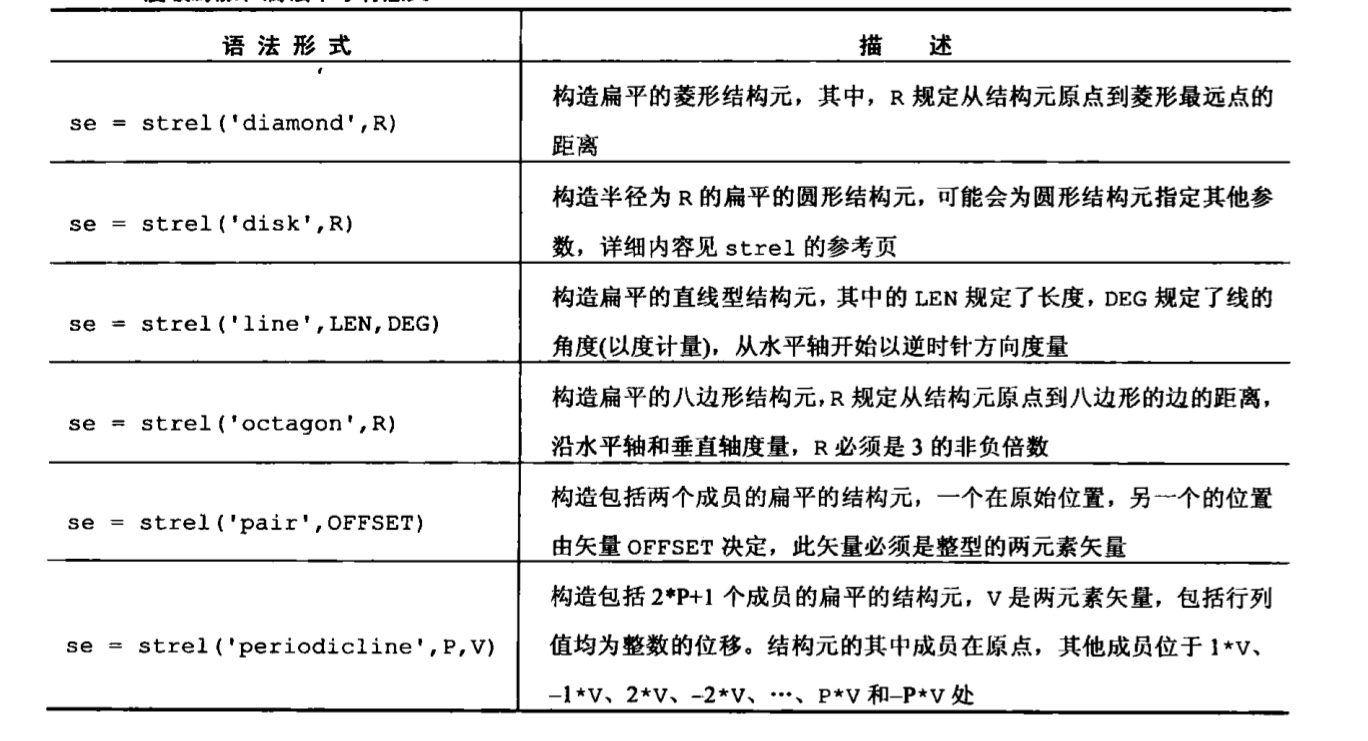

注意生成的se含有两项
- se.Neighborhood:[ × logical ]
- se.Demensionality: 2



