图像分割
基本边缘检测
边缘模型
- 台阶模型
在一个像素的距离上发生两次灰度级间理想的过渡 - 斜坡模型
数字图像存在被模糊或有噪声的边缘,这时的边缘被建模成一个更接近灰度斜坡的剖面,斜坡的斜度与边缘的模糊程度成反比 - 屋顶模型
通过一个区域的线的模型,屋顶边缘的基底(宽度)由该线的宽度和尖锐度决定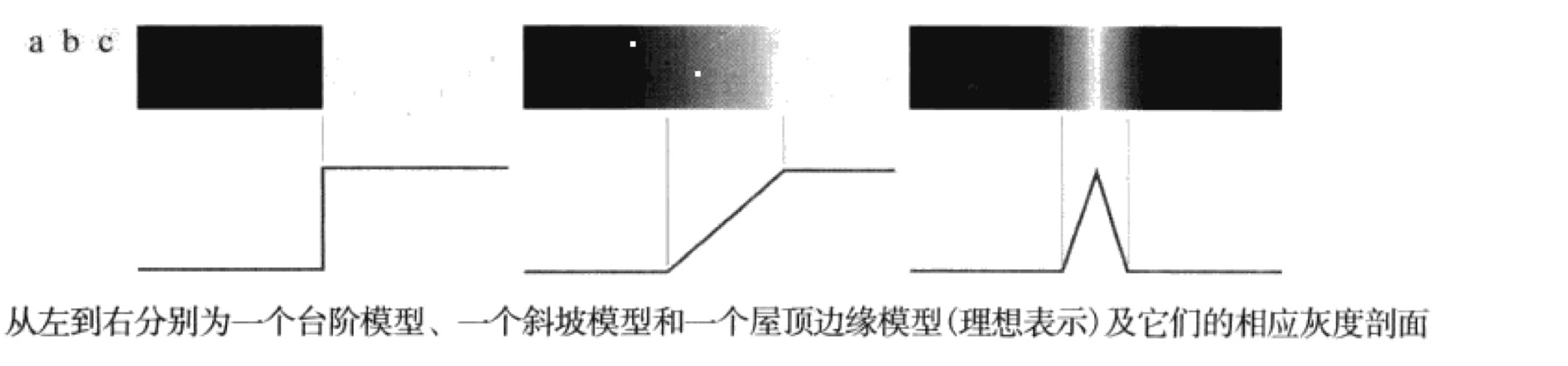
结合前面提到的一阶导数和二阶导数的性质,可以得出结论:
- 一阶导数的幅值可用于检测图像中的某个点处是否存在一个边缘
- 二阶导数的符号可用于确定一个边缘像素位于该边缘的暗的一侧还是亮的一侧
- 对图像的每个边缘,二阶导数生成两个值
- 二阶导数的零交叉点可用于定位粗边缘的中心
- 执行边缘检测的三个步骤:
- 为降噪对图像进行平滑处理
- 边缘点的检测
- 边缘定位
梯度
- 二维函数f(x,y)的梯度定义为一个向量:这个向量的幅值为了简化计算,通常省略平方根或取绝对值通常用梯度没的幅值或者近似值来简单作为’梯度’
梯度的性质是:梯度向量指向(x,y)坐标处f的最大变换率方向。最大变化率发生的角度是:
使用函数edge的边缘检测
- 语法
1
[g,t] = edge(f, 'method', parameters);
f是输入图像,method是边缘检测方法,parameters是附加参数
边缘检测算子
图像邻域如下图所示:
| $z_1$ | $z_2$ | $z_3$ |
|---|---|---|
| $z_4$ | $z_5$ | $z_6$ |
| $z_7$ | $z_8$ | $z_9$ |
Sobel边缘检测算子
- Sobel边缘检测算子模板
| -1 | -2 | -1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 2 | 1 |
| -1 | 0 | 1 |
|---|---|---|
| -2 | 0 | 2 |
| -1 | 0 | 1 |
每一行和每一列的中心像素用2来加权以提供平滑
- MATLAB语法
1
[g, t] = edge(f, 'sobel', T, dir);
f是输入的图像,T是指定的阀值,dir是指定的检测边缘的首选方向:’horizontal’,’vertical’,’both’(默认值)
t是可选的,T未指定,则t自动设置
Prewitt边缘检测算子
- Prewitt边缘检测算子模板
| -1 | -1 | -1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| -1 | 0 | 1 |
|---|---|---|
| -1 | 0 | 1 |
| -1 | 0 | 1 |
- MATLAB语法
1
[g, t] = edge(f, 'prewitt', T ,dir);
计算简单,但容易产生噪声
Roberts边缘检测算子
- Roberts边缘检测算子模板
| -1 | 0 |
|---|---|
| 0 | 1 |
| 0 | 1 |
|---|---|
| 1 | 0 |
- MATLAB语法
1
[g, t] = edge(f, 'roberts', T , dir);
LoG检测算子
- LoG
考虑高斯函数
$\sigma$是标准差。这是平滑函数,如果和图像卷积,会使图像变模糊,模糊程度由$\sigma$决定
这个函数的Laplace算法是:
用$\triangledown ^2G(x,y)$卷积(滤波)这幅图像与先用平滑函数对图像卷积,再对结果进行Laplace变换的结果是一样的
用$\triangledown ^2G(x,y)$卷积图像,可以得到两个效果:平滑图像(因而减少了噪声);计算Laplace,从而产生双边缘图像,然后在双边缘之间定位由发现的零交叉组成的边缘
- MATLAB语法
1
[g, t] = edge(f, 'log', T , sigma);
sigma默认值是2
零交叉检测算子
- 基于LoG,卷积使用特殊的滤波函数H来完成
- MATLAB语法
1
[g, t] = edge(f, 'zerocross', T , H);
Canny检测算子
- edge函数中最强的边缘检测算子
- MATLAB语法
1
[g, t] = edge(f, 'canny', T , sigma);
MATLAB实现
- 几种边缘检测算法的比较(Sobel,LoG,Canny)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22f = imread('timg1.jpg');
imshow(f),title('currect image');
f = rgb2gray(f);
%Default Output
[gSobel_default,ts] = edge(f, 'sobel');
[gLoG_default, tlog] = edge(f, 'log');
[gCanny_default, tc] = edge(f,'canny');
%Best Output
gSobel_best = edge(f,'sobel',0.165);
gLoG_best = edge(f,'log',0.008, 2.25);
gCanny_best = edge(f,'canny',[0.05, 0.4], 1.5);
figure,imshow(f),title('Gary images');
figure,imshow(gSobel_default),title('gSobel default');
figure,imshow(gSobel_best),title('gSobel best');
figure,imshow(gLoG_default),title('gLoG default');
figure,imshow(gLoG_best),title('gLoG best');
figure,imshow(gCanny_default),title('gCanny default');
figure,imshow(gCanny_best),title('gCanny best');
其中最佳输出的阀值是根据得到的ts,tlog,tc的值来确定的
结果:







综合结果来看,Canny边缘检测算子可以得到最好的结果
霍夫变换
介绍与应用场景
霍夫变换(Hough Transform)是图像处理中的一种特征提取技术,该过程在一个参数空间中通过计算累计结果的局部最大值得到一个符合该特定形状的集合作为霍夫变换结果。经典霍夫变换用来检测图像中的直线,后来霍夫变换扩展到任意形状物体的识别,多为圆和椭圆。霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值,从而把检测任意形状的问题转化为统计峰值问题。
基本原理
考虑点$(x_i,y_i)$及通过这个点的线,有无穷多的线通过点$(x_i,y_i)$,针对a和b的一些值,满足斜截式$y_i = ax_i + b$的所有线都通过该点。该公式也可以写为$b = -ax_i + y_i$,考虑ab平面(即参数空间)对固定点$(x_i,y_i)$得到一条线的方程。另外,第二个点$(x_j,y_j)$也有一条在参数空间中与之相关的线,这条线和与$(x_i,y_i)$相关的线交于点$(a’,b’)$,其中$a’$是斜率,$b’$是在xy平面上包含点$(x_i,y_i)$和$(x_j,y_j)$的线的截距。在参数空间中,这条线包含的所有点都有相交于$(a’,b’)$点的直线。
简单理解,直线由两个点$A(x_1,y_1)$和$B(x_2,y_2)$定义,在参数空间中,两条直线的唯一公共点是在原图像空间中表示连接点A和B的唯一存在的直线
因此,给定很多点,判断这些点是否共线的问题,经由霍夫变换之后,变成判断一堆曲线(每一个点在$(r, \theta)$平面上代表一条曲线)是否 在 $(r,\theta)$平面上相交于同一点的问题
另外用法线表示法:
水平线的$\theta$=0,$\rho$等于正的x的截距,垂直线的$\theta=90$度,$\rho$等于正的y的截距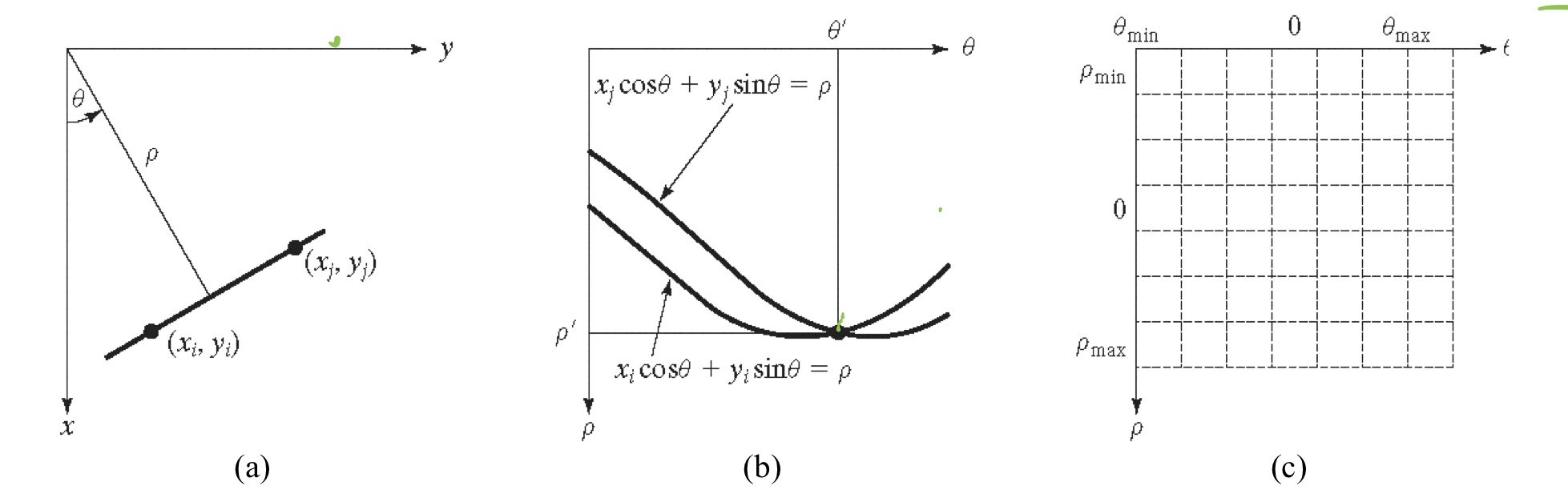
在坐标(i, j)的单元位置,累加器的值是 A(i, j),对应于参数空间坐标$(\rho_i,\theta_j)$的正方形。最初, 这些单元位置为零。然后,对于每个图像平面上的非背景点$(x_k,y_k)$(就是 xy 平面),我们令 θ 等 于在 θ 轴上允许的细分值,并通过公式$\rho = x_kcos\theta+y_ksin\theta$解出相应的 ρ 值。然后,得到的 ρ 值四 舍五入为最接近的 ρ 轴上允许的单元值。相应的累加器单元增加一个增量。在这个过程的最后, 累加单元 A(i, j)中的值 Q 就意味着 xy 平面上位于线$xcos\theta_j+ysin\theta_j = \rho_i$上的点有 Q 个。在$\rho\theta$平面上,细分的数目决定了这些点的共线的精确度。累加器数组在工具箱中叫做霍夫变换矩阵,简称霍夫变换。
MATLAB工具箱函数
hough函数
默认语法1
[H, theta, rho] = hough(f)
H是霍夫变换矩阵,theta和rho是$\theta$和$\rho$的值
下面这个例子可以加深对霍夫变换的理解1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21f = zeros(101,101);
f(1,1) = 1;
f(101,1) = 1;
f(1,101) = 1;
f(101, 101) = 1;
f(51, 51) = 1;
% H = hough(f);
[H, theta, rho] = hough(f);
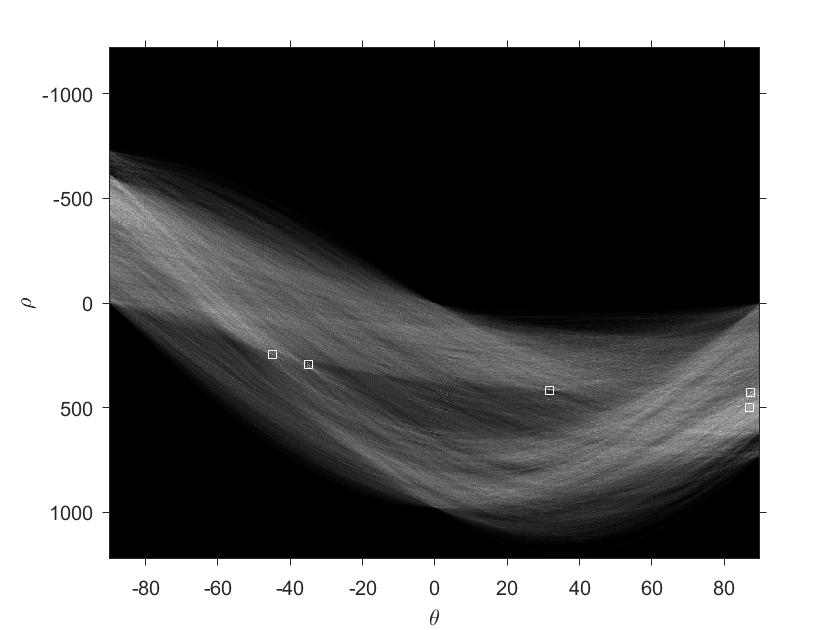
imshow(H, [],'XData', theta,'YData', rho, 'InitialMagnification', 'fit')
axis on, axis normal
xlabel('\theta'),ylabel('\rho')
结果: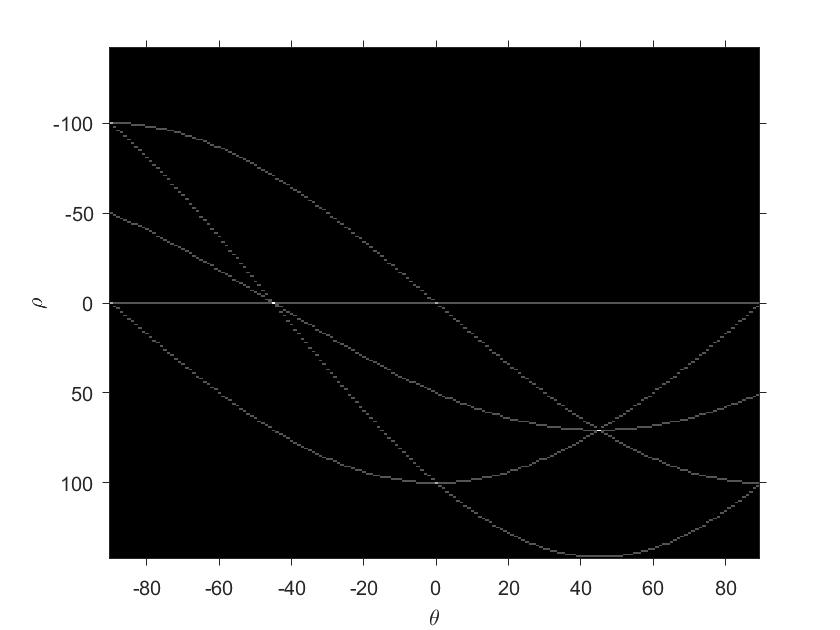
观察图可以看打到三条曲线在+45度和-45度处的交点指出:f中有两组三个共线的点。两条曲线在$(\rho,\theta)$ = (0,-90)、(-100,-90)、(0,0)、(100,0)处的交点指出:有4组位于垂直线和水平线上的公共点
houghpeaks函数
寻找指定的峰值数
默认语法1
peaks = houghpeaks(H, NumPeaks)
H是霍夫变换矩阵
houghlines函数
决定线的起点和终点
默认语法1
lines = houghlines(f, theta, rho, peaks)
输出lines是结构数组,长度等于找到的线段。结构中的每个元素可以看成一条线,并含有下列字段:
- point1:两元素向量[r1,c1],指定了线段终点的行列坐标。
- point2:两元素向量[r2,c2],指定了线段其他终点的行列坐标。
- theta:与线相关的霍夫变换的以度计量的角度。
- rho:与线相关的霍夫变换的$\rho$轴位置。
MATLAB使用霍夫变换检测和连接线
1 | f = imread('timg1.jpg'); |
结果: